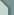- гиперкомплексные числа вида a+bе, где аи b- действительные числа, и для двойных чисел е 2= + 1, а для дуальных чисел е 2=0. Сложение Д. и д. ч. определяется формулой 
Умножение двойных чисел производится по формуле
а дуальных чисел - по формуле
Комплексные числа, двойные числа и дуальные числа наз. также комплексными числами гиперболического, эллиптического и параболического типов соответственно. Иногда при помощи этих чисел изображают движения трехмерных пространств Лобачевского, Римана и Евклида (см., напр., Винтовое исчисление).
Как двойные, так и дуальные числа образуют двумерные (с базой 1 и е)ассоциативно-коммутативные алгебры над полем действительных чисел. В отличие от поля комплексных чисел эти алгебры содержат делители нуля, причем в алгебре двойных чисел все делители нуля имеют вид 
Алгебра двойных чисел может быть разложена в прямую сумму двух полей действительных чисел. С этим свойством связано еще одно название двойных чисел - расщепляемые комплексные числа. Встречается и другое наименование двойных чисел - паракомплексные числа. Алгебра дуальных чисел рассматривается не только над полем Rдействительных чисел, но и над произвольным полем или коммутативным кольцом. Пусть A - коммутативное кольцо с единице и Месть А-модуль. Прямая сумма А-модулей А 
M. относительно умножения
является коммутативной А-алгеброй и обозначается IA (М). Она наз. алгеброй дуальных чисел относительно модуля М. A -модуль Мотождествляется с идеалом алгебры IA (М), служащим ядром пополняющего гомоморфизма
При этом квадрат М 2 данного идеала равен нулю, а 
Если А- регулярное кольцо, то верно и обратное: если Весть А-алгебра и М- идеал в Втакой, что M2=0 и 
то 
где Мрассматривается как А -модуль (см. [4]).
При М=А алгебра IA (М)(обозначаемая в этом случае IA )изоморфна факторалгебре алгебры многочленов (Т)по идеалу Т 2. Многие свойства A-модуля Мможно переформулировать как свойства алгебры 1A (М), что позволяет сводить многие вопросы об А-модулях к соответствующим вопросам в теории колец (см. [2]).
Если В- произвольная A-алгебра, 
- гомоморфизм и д:.
- дифференцирование В со значением в A-модуле М, рассматриваемом как В- модуль относительно гомоморфизма j, то отображение 
является гомоморфизмом А-алгебры. Обратно, для любого гомоморфизма A-алгебр f 
композиция 
где 
- проекция А на М, является A-дифференцированием Всо значением в М, рассматриваемом как B-модуль относительно гомоморфизма 
Это свойство Д. и д. ч. используется для определения касательного пространства к произвольному функтору на категории схем [1], [3].
Лит.:[1] Мамфорд Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [2] Fossum R., Trivial extensions of abelian categories, В., 1975; [3] Sсhemas en sroupes, I, B., 1970; [4] LichtenbaumS., Schlessinger M., "Trans. Amer. Math. Soc", 1967. v. 128, № 1, p. 41-70.
И. В. Долгачев.
